Comparison of two phonetic approaches to language identification
François Pellegrino, Jérôme Farinas, Régine
André-Obrecht
IRIT University Paul Sabatier
118 route de Narbonne, 31 062 Toulouse, France
(pellegri,jfarinas,obrecht)@irit.fr
http://www.irit.fr
Abstract
This paper presents two unsupervised approaches to Automatic Language Identification
(ALI) based on a segmental preprocessing. In the Global Segmental Model
approach, the language system is modeled by a Gaussian Mixture Model (GMM)
trained with automatically detected segments. In the Phonetic Differentiated
Model approach, an unsupervised detection vowel/non vowel is performed
and the language model is defined with two GMMs, one to model the vowel
segments and a second one to model the others segments. For each approach,
no labeled data are required. GMMs are initialized using an efficient data-driven
variant of the LBG algorithm: the LBG-Rissanen algorithm.
With 5 languages from the OGI MLTS corpus and in a closed set identification
task, we reach 85 % of correct identification with each system using 45
second duration utterances for the male speakers. We increase this performance
(91%) when we merge the two systems.
Keywords
Language Identification, vowel and consonant modeling.
1. Introduction
Automatic Language Identification (ALI) is one of the main challenges for
the next decade in automatic speech processing. Today, many efforts focus
on speech technology to provide reliable and efficient Human-Computer Interfaces.
The need for multilingual capacities becomes overwhelming because of the
joined development of world communication and multi-ethnic societies as
the European Economic Community.
The language obstacle will remain until ALI systems reach excellent
performance and reliability in order not to limit the overall system performance.
Presently, the most efficient ALI systems are based on phonotactic
discrimination via specific statistical language modeling [1,2,3,4].
In most of them, phonetic recognition is merely considered as a front-end:
it consists in a projection from the continuous acoustic space into a discrete
symbolic space without taking the resultant likelihood into account. This
approach may be sub-optimal from the phonetic and the phonological points
of view, though these aspects carry a substantial part of the language
identity.
We propose an alternative approach which emphasizes the rule of the
acoustic phonetic features. The acoustic processing consists of an a priori
automatic segmentation and a global analysis of each segment, followed
by a statistical decision:
-
for the Global Segmental Model system (GSM), the acoustic space of each
language is represented classically by an unique Gaussian Mixture Model
(GMM).
-
for the Phonetic Differentiated Model system, an a priori automatic identification
of the vocalic segments is performed. It results that, for each language,
the vocalic space is modeled by a GMM while the non vocalic space is modeled
by another one. The identification decision is given according to the combined
vocalic and non-vocalic likelihoods.
One advantage of such an approach is that no labeled data is necessary.
Experiments are realized with five languages (French, Japanese, Korean,
Spanish and Vietnamese) of the OGI Multilingual Telephone Speech corpus,
to compare the GSM and PDM systems; they obtain similar performance, but
the best performance results when merging them.
Section 2 of this paper offers a description
of the Global Segmental Model system, and section 3
a description of the Phonetic Differentiated Model one. Section
4 presents a number of experiments. We discuss the performance and
the perspective of such approaches during the conclusion
paragraph.
2. Global Segmental Model
The GSM system is described by two main components:
-
an acoustic processing which consists of:
-
a statistical segmentation of the speech in long steady units and short
transient ones.
-
a speech activity detection.
-
a cepstral analysis performed on each segment.
-
a decision procedure: the language is identified via a maximum likelihood
test provided by the language-dependent GMMs.
The same processing is applied during training and recognition.
2.1 The segmental pre processing
2.1.1 Segmentation and speech activity detection
The segmentation is provided by the "Forward-Backward Divergence" algorithm
[5] which is based on a statistical study of the acoustic
signal. Assuming that the speech signal is described by a string of quasi
stationary units, each one is characterized by an auto regressive Gaussian
model; the method consists in performing on line a detection of changes
in the auto regressive parameters. The use of an a priori segmentation
partially removes redundancy for long sounds, and a segment analysis is
very useful and relevant to locate coarse features. This approach has already
shown interesting results in automatic speech recognition; in particular,
experiments have proved that the segmental duration provides very useful
information [6].
The segmentation is followed by a Speech Activity Detection in order
to discard pauses. Each segment is labeled "silence" or "speech"; then
only speech segments are analyzed.
2.2 Cepstral analysis
Each segment is represented with a set of 8 Mel-Frequency Cepstral Coefficients
(MFCC) and 8 delta-MFCC. Cepstral analysis is performed using a 256-point
Hamming window centered on the segment. This parameter vector may be extended
with the duration of the underlying segment, the energy and delta-energy
coefficients. A cepstral subtraction performs both blind deconvolution
to remove the channel effect and speaker normalization.
2.2 Statistical framework
Let L = {L1, L2,…, LNL}
be the set of NL languages to identify; the problem
is to find the most likely language L* in L, given that the effective language
is really in this set (close set experiments).
Let T be the number of segments in the spoken utterance and O = {o1,
o2,…oT} be the sequence of observation vectors. Given
O and using Bayes' theorem, the most likely language L* according to the
model is: 
 |
(1) |
Additionally, if a priori language probabilities are assumed to be identical,
one gets the equation:
 |
(2) |
Under the standard assumptions, each segment is considered independent
of others, conditionally to the language model. Finally, L* is given in
the log-likelihood space by:
 |
(3) |
For each language Li, a GMM is trained with the set of detected speech
segments. The EM algorithm is used to obtain the maximum likelihood parameters
of each model [7]. This algorithm presupposes that the
number of the mixture components, Qi, and initial values for each Gaussian
pdf are given; in our system, the LBG and the LBG Rissanen algorithms fix
these parameters. During the recognition, the utterance likelihood is computed
with the detected speech segments.
2.2.1 Initializing GMM with the LBG algorithm
The LBG algorithm [8] elaborates a partition of the
observation space by performing an iterated clustering of the learning
data into codewords optimized according to the nearest neighbor rule. The
splitting procedure may be stopped either when the data distortion variation
drops under a given threshold or when a given number of codewords is reached.
2.2.2 Initializing GMM with the LBG Rissanen algorithm
The LBG-Rissanen algorithm is similar to the LBG algorithm except for the
iterated procedure termination. Before splitting, the Rissanen criterion
I(q) [9], function of the size q of the current codebook
is computed from the expression:
 |
(4) |
In this expression, Dq(X) denotes the log-distortion of the training
set X according to the current codebook, p the parameter space dimension
and N the cardinal of X.
Minimizing I(q) results in the optimal codebook size according to the
Rissanen information criterion. We use this data driven algorithm to determinate
independently the optimal number Qi of Gaussian pdfs for each language
GMM.
3. Phonetic Differentiated Model
In the PDM approach, language independent vowel detection is performed
prior to the cepstral analysis. The detection locates segments that match
vowel structure according to an unsupervised language-independent algorithm
[10]. For each language Li, a Vowel System GMM, VSi,
(respectively a Consonant System GMM, CSi) is trained with the set of detected
vowel segments (resp. non vowel segments).
Let T be the number of segments in the spoken utterance, obtained after
the acoustic processing and O = {o1, o2,…oT}
be a sequence of observation vectors. Each vector ok consists of a cepstral
vector yk and a macro-class flag ck, equal to 1 if the segment is detected
as a vowel, and equal to 0 otherwise. In order to simplify the formula,
we note ok={yk,ck}.
Since (ck) is a deterministic process, the most likely language
computed in the log-likelihood space is given by:
 |
(5) |
To train the VS and CS models, the procedure is the same as this used
for the training of the GSM. The EM algorithm is coupled to an initialization
of the number of components and the pdf parameters, by the LGB algorithm
or the LBG Rissanen algorithm.
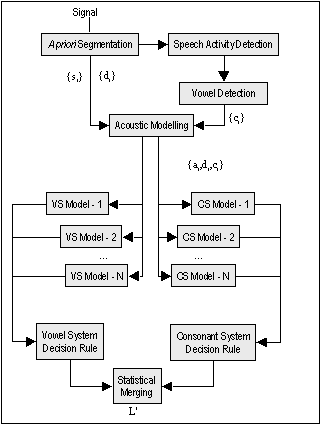 |
| Figure 1: Block diagram of the Phonetic Differentiated Model
system. The upper part represents the acoustic preprocessing and the lower
part the language dependent Vowel-System and Consonant-System Modelings. |
4. Experiments
4.1 Corpus description
The OGI Multilingual Telephone Speech [11] corpus has
been used in our experiments. The study is limited to 5 languages (French,
Japanese, Korean, Spanish and Vietnamese). The phonological differences
of the vowel system between these languages have motivated the use of this
subset. Spanish and Japanese vowel systems are rather elementary (5 vowels)
and quasi-identical while Korean and French systems are more complex. Vietnamese
system is of average size.
The data are divided into two corpora, namely the training and the
development sets. Each corpus consists in several utterances (constrained
and unconstrained). There are about 20 speakers per language in the development
subset and 50 speakers per language in the learning one. There is no overlap
between the speakers of each corpus. The identification tests are made
with a subset of the development corpus, called '45s' set, since 45s is
the mean duration of the utterances.
4.2 Global Segmental Model
Several acoustic analyses and the two initializations of the GMMs have
been assessed with the GSM system. The best results are obtained with 17
parameters: 8 MFCC, 8 delta MFCC and the duration of the segment. With
5 languages, the correct identification rate raises 86 % using the classical
LBG algorithm initialization: 50 Gaussian laws have been necessary. The
LBG-Rissanen algorithm hasn't bring any improvement: the optimal topology
of the GMM is difficult to find when we study the global acoustic space.
4.3 Phonetic Differentiated Model
To assess the VS models, a first sequence of experiments has been performed:
the most likely language L* is computed according to the only VS models;
the contribution of non vowel segments is equal to zero in the expression
(5).
When using the LBG algorithm, the best result is 67 % of correct identification
(with 20 Gaussian components by VS model). Using the LBG-Rissanen algorithm
to estimate the optimal size of each VS GMM is more efficient since the
identification rate reaches 78 %. This result shows that the modeling of
the vowel systems, is relevant and that the LBG-Rissanen approach is able
to determinate their convenient topology; remember that, in this case,
the size of each GMM depends of the language!
The same experiments have been performed to assess the CS models. The
best performance has been obtained when the initialization of the GMM is
realized by the LBG algorithm: 30 Gaussian components are necessary to
raise 78 % of correct identification. The LBG-Rissanen algorithm has provided
less discriminative models than those of constant size: consonant segments
are acoustically more heterogeneous than vowel segments; that means that
the consonant parameter space is much more complex than the vowel space
and the LBG-Rissanen is unable to deal with it.
The previous CS and VS models are combined to give the PDM approach
(equation 5); so a great number of experiments
have been necessary to define the best PDM system. The best one merges
the VS model initialized by the LBG Rissanen algorithm and the CS model
initialized by the classical LBG Rissanen. This merging has improved the
performance: 85 % of correct identification is reached.
4.4 GSM and PDM Comparison
As the previous experiments have shown, no significant differences, in
term of identification rate, arises between the PDM and GSM approaches
since they reach respectively 85% and 86% of correct identification (table
1).
| VS model |
CS model |
PDM |
GSM |
| 78 |
78 |
85 |
86 |
|
| table 1: Identification scores with all languages among 5 languages
(45s male utterances). |
In order to see if the information extracted from the signal by the
two approaches is redundant or complementary, another sequence of experiments
are performed to merge the different models.
The best performance is reached, when we combine the GSM system and
the VS model system: identification rate among 5 languages raises from
86 % to 91 % (table 2). The combination "CS model–GSM"
does not improve the results: consonantal information seems to be redundant
with GSM ones. When we merge the results of the GSM and the PDM, the results
are intermediate: the gain of the VS modeling is attenuated by the CS modeling.
Experiments have been done with 3 languages, in order to compare with
systems proposed in the literature. The figure 2 shows the results for
the male part of the test corpus and for the global test set. The mean
results are respectively 93.3 % and 86.4 %. This last result must be compared
to the 84% obtained by O. Andersen [12] and 91% by
S. Kadambe [13], where Hidden Markov Models (HMM) and
n-gram models have been used to model respectively the acoustic space and
the phonotactic level.
|
VS model |
CS model |
PDM |
| GSM |
91 |
86 |
88 |
|
| table 2: Identification scores obtained by merging the GSM and
the models issued from the phonetic differentiated approach (5 languages,
45s male utterances). |
5. conclusion
This work proves that a significant part of the language characterization
is embedded in its vowel system; the merging of the GSM and the VS model
shows that extracting and modeling this information is possible and efficient.
We will complete the notion of differentiated model, by introducing different
model structures (GMM, HMM) and different acoustic parameters dependent
of the phonetic classes (vowel, occlusive, fricative, et al). Then, to
compare this approach to the classical ones, it will be necessary to complete
our system with a phonotactic model, appropriate to our own acoustic projection.
6. References
[1] T. J. Hazen, & V. W. Zue, (1997), Segment-based
automatic language identification, Journal of the Acoustical Society of
America, Vol. 101, No. 4, pp. 2323-2331, April. [ps.gz,
pdf]
[2] L.F. Lamel, J.L. Gauvain, (1994), Language Identification
using Phone-Based Acoustic Likelihood, Proc. of ICASSP '94, Adelaide, pp.
293-296. [gzip]
[3] Y. Yan, E. Barnard & R. A. Cole, (1996), Development
of An Approach to Automatic Language Identification based on Phone Recognition,
Computer Speech and Language, Vol. 10, n° 1, pp 37-54, (1996) [ps.gz]
[4] M.A. Zissman, (1996), Comparison of four approaches
to automatic language identification of telephone speech. Proc. IEEE Trans.
on SAP, January 1996, vol. 4, n° 1. [abstract]
[5] R. André-Obrecht, (1988), A New Statistical
Approach for Automatic Speech Segmentation. IEEE Trans. on ASSP, January
88, vol. 36, n° 1.
[6] R. André-Obrecht, B. Jacob, (1997), Direct
Identification vs. Correlated Models to Process Acoustic and Articulatory
Informations in Automatic Speech Recognition, Proc. of ICASSP '97, Munich,
pp. 989-992. [pdf]
[7] A.P. Dempster, N.M. Laird, D.B. Dubin, (1977),
Maximum likelihood from incomplete data via the EM algorithm, J. Royal
statist. Soc. ServB.,39.
[8] Y. Linde, A. Buzo, R.M. Gray, (1980), An algorithm
for vector quantizer. IEEE Trans on Com., January 80, vol 28.
[9]J. Rissanen, (1983), An universal prior for integers
and estimation by minimum description length. The Annals of statistics,
vol 11, n° 2.
[10] F. Pellegrino, R André-Obrecht, (1997),
From vocalic detection to automatic emergence of vowel systems, Proc. ICASSP'97,
Munchen, April 1997. [pdf]
[11] T. L. Lander et al., (1995), The OGI 22 language
telephone speech corpus, Proc. Eurospeech’95, Madrid, pp. 817-820. [ps.gz]
[12] O. Andersen & P. Dalsgaard, Language-Identification
Based on Cross-Language Acoustic Models and Optimised Information Combination,
Proc. of Eurospeech '97, Rhodes, pp. 67-70, (1997) [pdf]
[13] S. Kadambe, J.L. Hieronymous, (1994), Spontaneous
speech language identification with a knowledge of linguistics, Proc. of
ICSLP'94, Yokohama, pp. 1879-1882.

