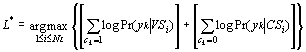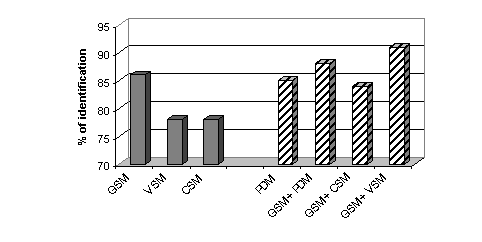VOWEL SYSTEM MODELING: A COMPLEMENT TO PHONETIC MODELING IN LANGUAGE IDENTIFICATION

François Pellegrino¹, Jérôme Farinas², Régine André-Obrecht²

¹DDL – ISH
14 avenue Berthelot, 69 363 Lyon Cedex 07
France
Francois.Pellegrino@univ-lyon2.fr

²IRIT University Paul Sabatier
118 route de Narbonne, 31 062 Toulouse
France
(jfarinas,obrecht)@irit.fr

ABSTRACT

Most systems of Automatic Language Identification are based on phonotactic approaches. However, it is more and more evident that taking other features (phonetic, phonological, prosodic, etc.) into account will improve performances. This paper presents an unsupervised phonetic approach that aims to consider phonological cues related to the structure of vocalic and consonantal systems.
In this approach, an unsupervised vowel/non vowel detection is used to model separately vocalic and consonantal systems. These Gaussian Mixture Models are initialized with a data-driven variant of the LBG algorithm: the LBG-Rissanen algorithm.
With 5 languages from the OGI MLTS corpus and in a closed set identification task, the system reaches 85 % of correct identification using 45 second duration utterances for male speakers. Using the vowel system modeling as a complement to an unsupervised phonetic modeling increases this performance up to 91 % while still requiring no labeled data.

1. INTRODUCTION

Until recently, Automatic Language Identification (ALI) was a marginal domain of automatic speech processing. The times are changing and today, it raises as one of the main challenges as far as Human-Computer Interfaces (HCI) are concerned. The need for multilingual capacities grows with the joined development of world communication and multi-ethnic societies as the European Economic Community. The language obstacle will remain until either multilingual large vocabulary continuous speech recognition or ALI systems reach excellent performance and reliability. Besides, video and audio contain-based indexing requires the extraction of extra linguistic information (music/speech segmentation, speaker and language identification).
Presently, the most efficient ALI systems are based on phonotactic discrimination via specific statistical language modeling [1,2,3,4]. In most of them, phonetic recognition is merely considered as a front-end: it consists in a projection of the continuous acoustic space into one or several discrete sets corresponding more or less to phonetic units. Though this approach achieves the best results, it seems that increasing performances necessitates to take additional features (especially phonetic ones) into account.
Obviously, if these features have been neglected for a while, it is because they are not so easy to exploit in ALI. Efficient phonetic modeling, based mainly on Hidden Markov models (HMM) used to require a consequent amount of hand-labeled data for training. Unfortunately, this kind of data is expensive to acquire and it is available only for a few languages (6 in the Multi Language Telephone Speech database from OGI [5]). Consequently, phonetic based systems were limited to these 6 languages. Fortunately, HMM reach today better performances and enhanced capacity of adaptation while requiring less and less hand-labeled data: phonetic modeling becomes a competitive approach and reaches good results [6].
Exploiting both phonetic and phonotactic cues is a very efficient approach, but we think that it may be significantly improved by taking phonology in consideration, especially for languages where no labeled data are accessible. For such languages, we propose to emphasize the structure of their phonological systems. This approach consists in two steps:
- splitting the speech utterance in segments corresponding with natural sound categories (vowels, fricatives, etc.) and then
- modeling each category as a whole, in order to capture the salient phonological cues of the language.
Linguists are collecting language descriptions and developing language typologies for a while [7]. We think that taking advantage of phonological typologies is a promising approach both for ALI and for automatic language description.
The aim of the experiments that are reported in this paper is to assess the discriminative power of an unsupervised phonological approach.
Next section will describe briefly the two systems (a global segmental model or GSM and a Phonetic Differentiated Model or PDM) which are used in the experiments. Each model is then described in details (Sections 3 and 4). Experiments on the OGI MLTS database are reported in Section 5. We discuss the performance and the perspective of such approaches in the conclusion paragraph.

2. DESCRIPTION OF THE SYSTEMS

Two systems have been implemented for these experiments.
In the first one, all the utterances of a given language are segmented, gathered and modeled by a single Gaussian Mixture Model (GMM) evaluated in a cepstral space. This Global Segmental Model (GSM) is partially similar to the simplest model proposed by M. Zissman in [4] and is used as a reference system.
The second model is an extension of the first one, but it is designed to test the hypothesis that the structural information on the vowel system of each language can be modeled to identify it. A vowel detection algorithm is used to split the segments gathered for each language in 2 categories : vowel and non-vowel. For each language, one GMM is subsequently evaluated from each set : a Vowel System Model (VSM) and a Consonantal System Model (CSM) though non-vowel segments can not be exactly considered as consonants (vowel transitions may also be labeled as non-vowels).
The choice of the vowel/non-vowel distinction is based on both linguistic and acoustic considerations: from a linguistic point of view, vowel system typologies are available for a few years [8]. Additionally, the homogeneous structure of the vocalic acoustic space provides a good framework to investigate structure modeling.
Both systems take advantage from an a priori segmentation algorithm [9]. It provides variable length segments by detecting ruptures in the statistical structure of the speech signal. This way, a duration information is provided for each sound prior to any additional modeling.

3. GLOBAL SEGMENTAL MODEL

The idea of modeling all the sounds of a language in a single model is not new. It has been first proposed in the 80’s and M. Zissman has implemented it in [4]. The goal is to model the phonetic space of each language rather than each phone. The advantage is that it does not require any knowledge on the allophones for each language. Unfortunately, it tends to be less discriminative than a phone modeling approach. However, taking the duration provided by the a priori segmentation into account may enhance the performances as it is used to in speech recognition experiments [10].

3.1 Statistical framework

Let L = {L₁, L₂,…, L_NL} be the set of NL languages to identify; the problem is to find the most likely language L* in L, given that the effective language is really in this set (closed set experiments).

Let T be the number of segments in the spoken utterance and O = {o₁, o₂,…o_T} the sequence of observation vectors. Given O and using Bayes' theorem, the most likely language L* according to the model is:

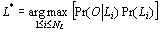(1)

Additionally, if a priori language probabilities are assumed to be identical, one gets the equation:

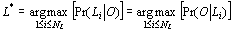(2)

Under the standard assumptions, each segment is considered independent of the others, conditionally to the language model. Finally, L* is given in the log-likelihood space by:

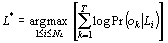(3)

For each language Li, a GMM is trained with the set of speech segments. The EM algorithm is used to obtain the maximum likelihood parameters of each model [11]. This algorithm presupposes that the number of the mixture components, Qi, and initial values for each Gaussian probability density functions are given; in our system, the LBG [12] and/or the LBG Rissanen algorithms [13] fix these parameters. During the recognition, the utterance likelihood is computed with the speech segments according to each language-specific model.

3.2 GSM Implementation

The training procedure consists in the following processing:

An a priori segmentation provides long steady and shorter transient segments.
A speech activity detector is applied to discard pauses.
A segmental cepstral analysis is performed on each segment.
One GMM per language is estimated with the set of language dependent observations.

Note that, unlike most acoustic-phonetic decoders, the cepstral analysis is performed on variable length segments rather than on constant duration frames; the segment duration is added to the observation vector.

The same acoustic processing is applied during recognition, and the language is identified via a maximum likelihood computation of the utterance according to the language dependent models.

3.2.1 Segmentation and speech activity detection

The segmentation is provided by the "Forward-Backward Divergence” algorithm [9] which is based on a statistical study of the acoustic signal. Assuming that the speech signal is described by a string of quasi stationary units, each one is characterized by an auto regressive Gaussian model; the method consists in performing an on line detection of changes in the auto regressive parameters. The use of this segmentation partially removes redundancy for long sounds, and a segment analysis is very useful and relevant to locate coarse features.
The segmentation is followed by a Speech Activity Detection in order to discard pauses. Each segment is labeled "silence" or "speech"; long silences (longer than 150 ms) are considered as non-speech and subsequently discarded.

3.2.2 Cepstral analysis

Each segment is characterized by a set of 8 Mel-Frequency Cepstral Coefficients (MFCC) and 8 delta-MFCC. Cepstral analysis is performed using a 256-point Hamming window centered on the segment. This parameter vector may be extended with the duration of the underlying segment. A cepstral subtraction performs both blind deconvolution to remove the channel effect and speaker normalization.

3.2.3 GMM Modeling

Initializing GMM with the LBG algorithm

The LBG algorithm [12] elaborates a partition of the observation space by performing an iterated clustering of the learning data into codewords optimized according to the nearest neighbor rule. The splitting procedure may be stopped either when the data distortion variation drops under a given threshold or when a given number of codewords is reached. This last procedure has been used in our experiments.

Initializing GMM with the LBG Rissanen algorithm

The LBG-Rissanen algorithm is similar to the LBG algorithm except for the iterated procedure termination. Before splitting, the Rissanen criterion J(q) [13, 14], function of the size q of the current codebook is computed from the expression:

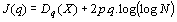(4)

In this expression, Dq(X) denotes the log-distortion of the training set X according to the current codebook, p the parameter space dimension and N the cardinal of X.
Minimizing J(q) results in the optimal codebook size according to the Rissanen information criterion. We use this data-driven algorithm to determinate automatically the optimal number Qi of Gaussian pdfs for each language.

3.2.4 Recognition processing

During the identification phase, the utterance is processed the same way, and its likelihood is computed according each language model using the speech segments. According to equation (3), the maximum likelihood rule is applied.

4. PHONETIC DIFFERENTIATED MODEL

In the PDM approach, language independent vowel detection is performed prior to the cepstral analysis. The detection locates segments that match vowel structure according to an unsupervised language-independent algorithm [15]. For each language Li, a Vowel System GMM, VSi, (respectively a Consonantal System GMM, CSi) is trained with the set of detected vowel segments (resp. non-vowel segments).

Figure 1 - Block diagram of the Phonetic Differentiated Model system. The upper part represents the acoustic preprocessing and the lower part the language dependent Vowel and Consonant-System Modeling.

4.1 Statistical framework

Let T be the number of segments given by the segmentation in the spoken utterance and O = {o₁, o₂,…o_T} be a sequence of observation vectors. Each vector ok consists of a cepstral vector yk and a macro-class flag c_k, equal to 1 if the segment is detected as a vowel, and equal to 0 otherwise. In order to simplify the formula, we note o_k={y_k,c_k}.
Since (ck) is a deterministic process, the most likely language computed in the log-likelihood space is given by:

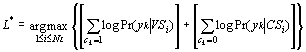(5)

4.2 PDM Implementation

Vowel detection is based on a spectral analysis algorithm. It is language independent and no training procedure is required.
To train the VS and CS models, the procedure is the same as the one used for training the GSM. The EM algorithm is combined with an initialization, by the LBG algorithm or the LBG-Rissanen algorithm.
In recognition phase, the utterance are processed the same way. It provides two sets of observations (vowel and non-vowel segments). For each language, two likelihoods are computed, according to the VS and the CS models. The maximum likelihood rule is applied to the overall likelihood (computed according to equation 5).

5. EXPERIMENTS

5.1 Corpus description

The OGI MLTS corpus [5] has been used in our experiments. The study is currently limited to 5 languages (French, Japanese, Korean, Spanish and Vietnamese). The phonological differences of the vowel system between these languages have motivated the use of this subset [8]. Spanish and Japanese vowel systems are rather elementary (5 vowels) and quasi-identical. Korean and French systems are quite complex, and they make use of secondary articulations (long vs. short vowel opposition in Korean and nasalization in French). Vietnamese system is of average size.
The aim of this corpus is to estimate the discriminative power of vowel system modeling if the phonological VS are close or if salient features are available (e.g. nasal vowels).
The data are divided into two corpora, namely the training and the development sets. Each corpus consists in several utterances (constrained and unconstrained). There are about 20 speakers per language in the development subset and 50 speakers per language in the learning one. There is no overlap between the speakers of each corpus. The identification tests are made with a subset of the development corpus, called ‘45s’ set, since 45s is the mean duration of the utterances.

5.2 Global Segmental Model

Several acoustic analyses and the two procedures of initialization have been assessed with the GSM system. Preliminary experiments have shown that taking the segment duration into account always improves performances. With 5 languages, the correct identification rate raises 86 % using the classical LBG algorithm initialization with the codebook size constrained.

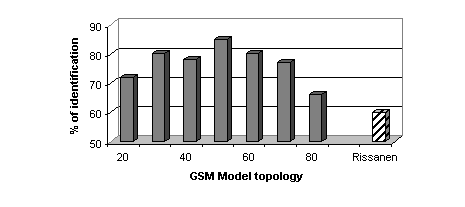Figure 2 – Correct identification rate as a function of the GSM model topology. Dash bar corresponds with GSM initialized by LBG-Rissanen and plain bars with LBG algorithm (the a priori codebook size is displayed).

These results are obtained with 50 Gaussian laws for each language. The LBG-Rissanen algorithm is quite inefficient (see Figure 2). It does not handle correctly with the complexity of the global acoustic space and it is trapped, resulting in ineffective codebook sizes smaller than the expected ones (see Table 1).

5.3 Phonetic Differentiated Model

5.3.1 Vowel system modeling

To assess the VS models, a first sequence of experiments has been performed: the most likely language L* is computed according to the VS models and non-vowel segments are discarded. When using the LBG algorithm, the best result is 67 % of correct identification (with 20 Gaussian components by VS model). Using the LBG-Rissanen algorithm to estimate the optimal size of each VS GMM is more efficient since the identification rate reaches 78 % (Figure 3). Remembering that only vowel segments are used (i.e. less than 10 seconds per utterance), this result shows that the VSM coupled with the LBG-Rissanen algorithm is able to correctly capture the structure of the vowel systems unlike what happened with GSM: Codebook sizes determined by LBG-Rissanen are significantly higher and the joined performances are much better for VSM than for GSM (see Table 1).

	French	Japanese	Korean	Spanish	Vietnamese
GSM	15	12	12	20	10
VSM	29	24	23	22	21
CSM	22	23	24	25	27

Table 1 - Language-dependent model size given by LBG-Rissanen algorithm as a function of the parameter set (global, vocalic or consonantal).

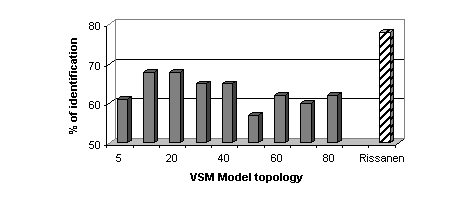Figure 3 – Correct identification rate as a function of the VSM model topology. Dash bar corresponds with VSM initialized by LBG-Rissanen and plain bars with LBG algorithm (the a priori codebook size is displayed).

5.3.1 Consonant system modeling

The same kind of experiments have been performed to assess the CS models. Non-vowel segments are used (about 25 seconds per utterance). The best performance has resulted from the initialization of the GMM with the LBG algorithm: 30 Gaussian models reach 78 % of correct identification (Figure 3). The LBG-Rissanen algorithm has provided less discriminative models than those of constant size: consonant segments are acoustically more heterogeneous than vowel segments; as a consequence, the consonant parameter space is much more complex than the vowel space and the LBG-Rissanen is unable to deal with it, similar to its behavior with the GSM.

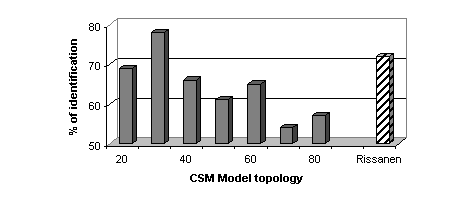Figure 4 – Correct identification rate as a function of the CSM model topology. Dash bar corresponds with GSM initialized by LBG-Rissanen and plain bars with LBG algorithm (the a priori codebook size is displayed).

5.3.1 Phonetic Differentiated Modeling

The previous CS and VS models are combined to give the PDM approach (equation 5); The best system merges the VS model initialized by the LBG Rissanen algorithm and the CS model initialized by the classical LBG. 85 % of correct identification is reached.

5.4 GSM and PDM Comparison

As the previous experiments have shown, no significant differences, in term of identification rate, arises between the PDM and GSM approaches since they reach respectively 85% and 86% of correct identification (Table 2).

VSM	CSM	PDM	GSM
78	78	85	86

Table 2 – Identification scores with all languages among 5 languages (45s male utterances).

In order to see if the information extracted from the signal by the two approaches is redundant or complementary, another sequence of experiments are performed to merge the different models. Scores provided by the considered models are combined and the maximum score is selected.
The best performance is reached when the GSM system and the VS model system are merged: identification rate among 5 languages raises from 86 % to 91 % (see Figure 5). The combination "CS model–GSM" does not improve the results: consonantal information seems to be redundant with GSM ones. When we merge the results of the GSM and the PDM, the results are intermediate: the gain of the VS modeling is attenuated by the CS modeling.

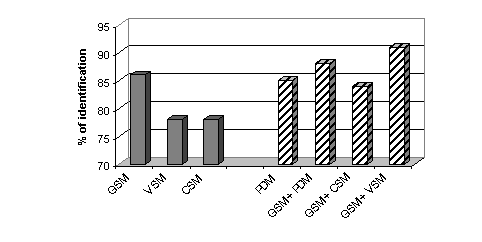Figure 5 – % of correct identification according to the models. Dash bars correspond with systems resulting from merging.

The improvement of performance when using VSM as a complement to GSM is statistically significant. Additional experiments have been done to investigate if it is due to the redundant use of the vowel segments (resulting in a double weight with respect to consonantal segments) or if the VSM brings additional information. They confirm that the improvement is not an artifact of the weighting factor applied to vowel segments. Thus, the structure of the vowel system is a discriminative feature that is complementary to global phonetic modeling.
Additional experiments have been done with 3 languages, in order to compare with systems proposed in the literature. The figure 6 shows the results for the male part of the test corpus and for the global test set. The mean results are respectively 93.3 % and 86.4 %. This last result must be compared to the 84% obtained by O. Andersen [16] and 91% by S. Kadambe [17], where Hidden Markov Models (HMM) and n-gram models have been used to model respectively the acoustic space and the phonotactic level.

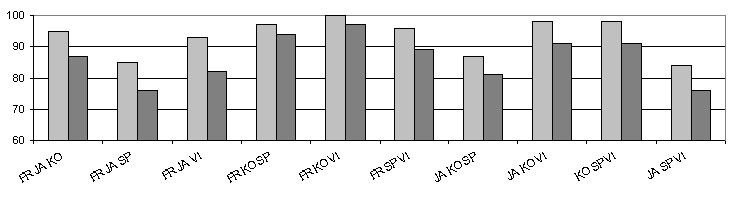
Figure 6 - Identification rate for a 3 language identification task, and the '45s' test set. (in light, the test is limited to the male speaker set, while in dark, both male and female speakers are considered). Note that the models have been trained only with male speakers.

6. CONCLUSION

This work proves that a significant part of the language characterization is embedded in its vowel system: vowel segments seem to be highly discriminative since the same level of performance is reached with vowel system modeling and consonantal system modeling though the consonantal duration is twice the vocalic duration in the utterances. Moreover, vowel system modeling using the LBG-Rissanen algorithm provides additional identification cues that are not exploited in the global segmental model (GSM). Thus, merging of the GSM and the VSM shows that extracting and modeling this information is possible and efficient.
The interest of the differentiated modeling approach is actual, and many advantages of the use of acoustic modeling in homogeneous spaces may be pointed out:

Minimum Description Length algorithms (like LBG-Rissanen) are able to handle with the structure of the acoustic-phonetic system.

A better discrimination is reached inside each model.

The parameter space can be adapted to the characteristics of the acoustic class that is modeled

We will complete the notion of differentiated model, by introducing different model structures (GMM, HMM) and different acoustic parameters dependent of the phonetic classes (occlusive, fricative, et al). Then, to compare this approach to the classical ones, it will be necessary to complete our system with a phonotactic model, appropriate to our own acoustic projection.

7. REFERENCES

[1] T. J. Hazen, & V. W. Zue, (1997), Segment-based automatic language identification, Journal of the Acoustical Society of America, Vol. 101, No. 4, pp. 2323-2331, April. [ps.gz, pdf]

[2] L.F. Lamel, J.L. Gauvain, (1994), Language Identification using Phone-Based Acoustic Likelihood, Proc. of ICASSP '94, Adelaide, pp. 293-296. [ps.gz]

[3] Y. Yan, E. Barnard & R. A. Cole, (1996), Development of An Approach to Automatic Language Identification based on Phone Recognition, Computer Speech and Language, Vol. 10, n° 1, pp 37-54, (1996) [ps.gz]

[4] M.A. Zissman, (1996), Comparison of four approaches to automatic language identification of telephone speech. Proc. IEEE Trans. on SAP, January 1996, vol. 4, n° 1. [abstract]

[5] Y. K. Muthusamy, R. A. Cole & B. T. Oshika, (1992), The OGI Multilingual Telephone speech Corpus, Proc. of ICSLP '92, Banff, pp. 895-898 [ps.gz]

[6] D. Matrouf, M. Adda-Decker, J.-L. Gauvain & L. Lamel, (1999), Identification automatique de la langue par téléphone, actes de la 1ère Journée d’étude du GFCP sur l’identification automatique des langues, Lyon.

[7] I. Maddieson, (1986), Patterns of sounds, 2nd Edition, Edited by Cambridge Univ. Press, USA

[8] N. Vallée, (1994), Systèmes vocaliques : de la typologie aux prédictions, Thèse de 3ème cycle, Univ. Stendhal, Grenoble

[9] R. André-Obrecht, (1988), A New Statistical Approach for Automatic Speech Segmentation. IEEE Trans. on ASSP, January 88, vol. 36, n° 1.

[10] R. André-Obrecht, B. Jacob, (1997), Direct Identification vs. Correlated Models to Process Acoustic and Articulatory Informations in Automatic Speech Recognition, Proc. of ICASSP '97, Munich, pp. 989-992. [pdf]

[11] A.P. Dempster, N.M. Laird, D.B. Dubin, (1977), Maximum likelihood from incomplete data via the EM algorithm, J. Royal statist. Soc. ServB.,39.

[12] Y. Linde, A. Buzo, R.M. Gray, (1980), An algorithm for vector quantizer. IEEE Trans on Com., January 80, vol 28.

[13] J. Rissanen, (1983), An universal prior for integers and estimation by minimum description length. The Annals of statistics, vol 11, n° 2.

[14] N. Parlangeau, F. Pellegrino and R. André-Obrecht (1999), Investigating Automatic Language Discrimination via Vowel System And Consonantal System Modeling, Proc. of ICPhS ’99, San Francisco. [doc.zip, ps.gz]

[15] F. Pellegrino, R André-Obrecht, (1997), From vocalic detection to automatic emergence of vowel systems, Proc. ICASSP'97, Munchen, April 1997. [pdf]

[16] O. Andersen & P. Dalsgaard, Language-Identification Based on Cross-Language Acoustic Models and Optimised Information Combination, Proc. of Eurospeech '97, Rhodes, pp. 67-70, (1997) [pdf]

[17] S. Kadambe, J.L. Hieronymous, (1994), Spontaneous speech language identification with a knowledge of linguistics, Proc. of ICSLP'94, Yokohama, pp. 1879-1882.